В §21 мы с вами рассмотрели описание воздействия на тело двух сил, если эти силы направлены вдоль одной прямой, научились вычислять равнодействующую таких сил.
Однако часто на тело действует несколько других тел, причем их воздействие направлено под разными углами друг к другу (рис. 1 и 2):
Можно ли сложить такие силы и рассмотреть равнодействующую сил, направленных под углом друг к другу?
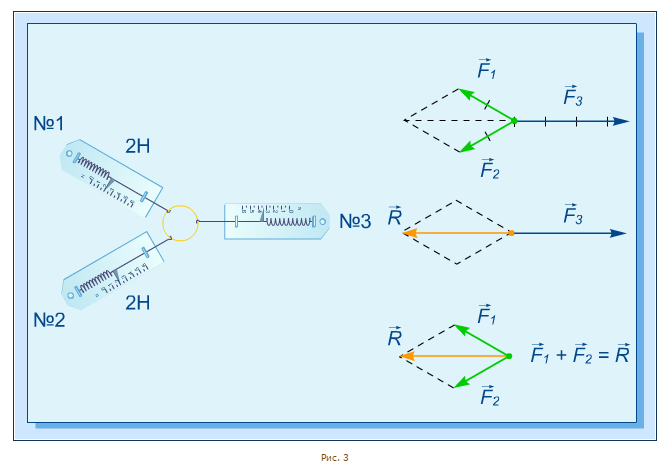
Для ответа на вопрос обратимся к эксперименту. Крючками двух динамометров зацепим колечко так, чтобы они воздействовали на кольцо под углом друг к другу. Чтобы скомпенсировать воздействие этих двух сил, приложим с противоположной стороны третий динамометр и зафиксируем его показания (рис. 3):
Оказывается, показание динамометра № 3, то есть числовое значение силы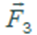 
, таково, что его длину можно получить, построив на векторах 
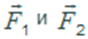фигуру, показанную на рисунке. Такая фигура с четырьмя углами получается, если перенести векторы 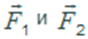параллельно самим себе, и называется поэтому параллелограммом. Причем такая закономерность наблюдается при любых углах между силами 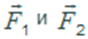и при любых числовых значениях этих сил. Свойства такого четырехугольника-параллелограмма вы будете изучать на уроках геометрии. Отрезок прямой, соединяющий вершины противоположных углов, называется диагональю параллелограмма.
Таким образом, числовое значение силы 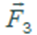всегда равно длине диагонали параллелограмма, построенного на векторах, длины которых, как мы помним, в определенном масштабе равны показаниям динамометров № 1 и № 2.
Поскольку силу 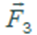можно скомпенсировать силой 
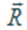, направленной противоположно и численно равной силе 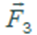, то, значит, сила 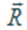производит на кольцо такое же действие, как две силы 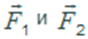, то есть является равнодействующей этих сил. Таким образом, эксперимент дает правило:
Равнодействующая двух сил 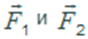, направленных под углом друг к другу, направлена по диагонали параллелограмма, построенного на этих векторах как на сторонах, и равна численно длине диагонали этого параллелограмма.
Равнодействующая сил 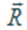называется суммой сил 
.
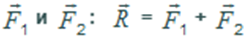Это правило называется правилом параллелограмма для сложения векторов.
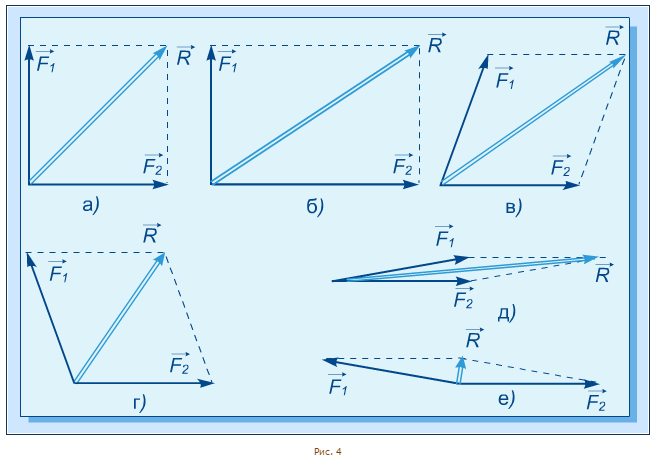
На рис. 4 показано построение вектора 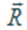равнодействующей сил 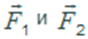в разных случаях: когда силы расположены под углом 90° (рис. 4а и б), под острым (рис. 4 в, д) и тупым (рис. 4 г, е) углом друг к другу.
Рисунки 4д и 4е показывают, что правило параллелограмма переходит в закон сложения сил, направленных по одной прямой ( §21), если угол между векторами приближается к 0° (векторы направлены в одну сторону) или к 180° (векторы направлены в противоположные стороны).
Правило параллелограмма верно для всех векторных физических величин, а не только для векторов сил, поэтому в математике оно называется правилом сложения векторов. Однако требуется понимать взаимосвязь векторных физических величин с реальными явлениями, которые они описывают. Например, если речь идет о двух силах, действующих на первоначально покоящееся тело, то направление равнодействующей, найденное по правилу параллелограмма, показывает, куда направлено суммарное воздействие этих двух сил, то есть куда начнет двигаться покоящееся тело.
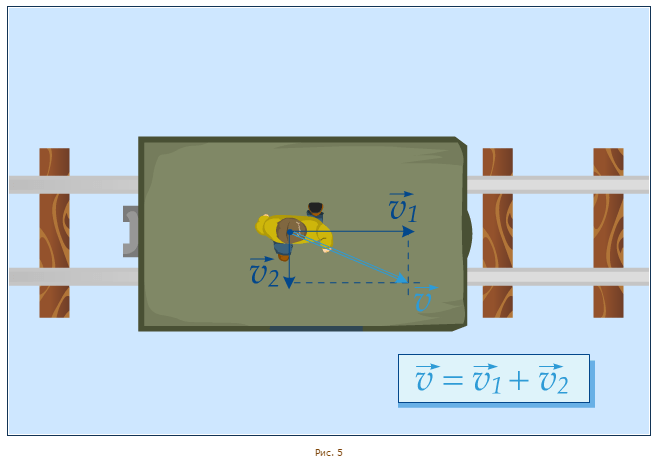
Можно воспользоваться правилом параллелограмма и для сложения векторов скорости. Например, если железнодорожная платформа движется по рельсам со скоростью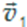 
, а человек идет относительно платформы со скоростью 
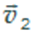в перпендикулярном направлении, то, складывая векторы скорости по правилу параллелограмма, можно найти вектор 
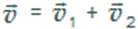, то есть узнать, в каком направлении человек, участвующий в таком сложном движении, перемещается относительно Земли (рис. 5).
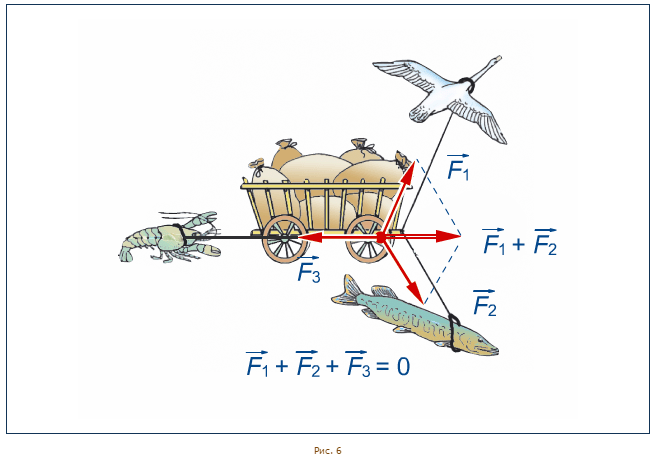
В заключение отметим, что, применив правило параллелограмма несколько раз, можно складывать и три, и большее количество сил. Для этого надо найти по правилу параллелограмма сумму двух сил, а затем этот суммарный вектор сложить по правилу параллелограмма с третьим вектором. Так, на рис. 6 показано, что в споре лебедя, рака и щуки победителей нет, поскольку равнодействующая трех сил, действующих на воз, равна нулю, или, другими словами, равнодействующая сил, описывающих воздействие лебедя и щуки, равна по величине и направлена противоположно силе воздействия рака.
Написать письмо
Очень интересное объяснение материала, это не входит в программу но очень простое объяснение сложной темы